工作室 99 ハノイの塔
ちょうど30年前になりますが、ハノイの塔の解法プログラムを作ったことがありました。なぜ、そんなことを思い出したのかというと、近頃iOS9がどうのこうのという話題がネットで流れているのを見かけたからです。そう、30年前に使っていたのがOS9というOSでした。当時使っていた富士通のFM11AD2というパソコンのOSです。モトーローラ社のCPU6809用のOSなのでOS9という名称でした。その言語でBASIC09というのがあって、これでハノイの塔の解法プログラムを作ったのです。こういうプログラムは自分自身を子プロセスとして呼び出す再帰的呼び出し(recursic call)が使えないとできません。BASIC09は名前だけはBASICと付いていますがどちらかというとパスカルのような言語でした。
30年前は仮想的なものでしたが、今回は思い出しついでにと、そのハノイの塔を実際に作ってみることにしました。PCのプログラムを作って画面上で動かすのと、実際に物を手でつかんで動かすのはまったく違います。30年も経ってからこんな事になるなんて、当時はまったく思いもしませんでした。実際にハノイの塔を見たことも触ったこともありませんし、自分で作れるなんて想像もしませんでした。プログラムを書くのは指先でキーボードを打つだけですが、実際に木を切ったり孔を空けたり塗料を塗ったりという作業は物を作っているなぁと言う実感があります。

設計
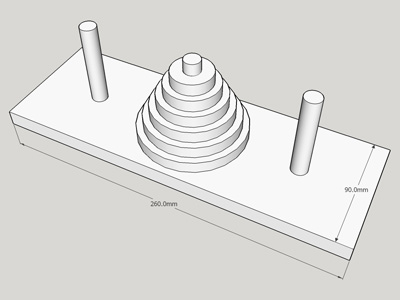
いつものようにSketchUpで設計しました。
左の画像をクリックするとダウンロードできます。SketchUp Viewerで任意の向きに回転させたり拡大縮小したりして観ることができます。
製作

厚さ12mm幅90mmの板を260mmに切って、12mmの孔を三っつ空けます。

12mmの丸棒を75mmに三本切ります。

9mm厚の板に80mm,70mm,60mm,50mm,40mm,30mmの円を描き、中心に14mmの孔を空けます。

円盤を6枚切り出します。

棒を立ててみました。角張っているので、ちょっと引っかかったりします。

そこで、このように先端をとがらせてみました。

三本の棒を立てて接着します。

きれいにやすりがけをしてなめらかに抜き差しできるようにしました。
完成

レモンオイルを塗って完成です。
遊び方
ルールは二つだけです。
- 一度に一枚だけしか動かしてはいけない。
- 小さい円盤に大きい円盤を載せてはいけない。
基本3枚の動かし方

円盤は6枚作りましたが、基本の動かし方はこの3枚です。よくネットに上がっているのは左端から右端への動かし方ですが、ここでは右端から左端への動かし方を披露いたします。
上に書いた二つのルールを守って動かします。3枚だとこのように7手で完了します。
6枚の動かし方

では、6枚だと何手になるでしょうか。
図のように位置をABC。円盤を上から順に1,2,3,4,5,6として動きを追ってみましょう。

第1手
1 -> B
最初の一手でどこに移動するか。これが肝心です。まあ、間違えても完成はできるのですが、手数が増えます。

第2手
2 -> A

第3手
1 -> A

第4手
3 -> B

第5手
1 -> C

第6手
2 -> B

第7手
1 -> B

第8手
4 -> A

第9手
1 -> A

第10手
2 -> C

第11手
1 -> C

第12手
3 -> A

第13手
1 -> B

第14手
2 -> A

第15手
1 -> A

第16手
5 -> B

第17手
1 -> C

第18手
2 -> B

第19手
1 -> B

第20手
3 -> C

第21手
1 -> A

第22手
2 -> C

第23手
1 -> C

第24手
4 -> B

第25手
1 -> B

第26手
2 -> A

第27手
1 -> A

第28手
3 -> B

第29手
1 -> C

第30手
2 -> B

第31手
1 -> B

第32手
6 -> A
やっとここで最下段の6枚目を左端に移動できました。

第33手
1 -> A

第34手
2 -> C

第35手
1 -> C

第36手
3 -> A

第37手
1 -> B

第38手
2 -> A

第39手
1 -> A

第40手
4 -> C

第41手
1 -> C

第42手
2 -> B

第43手
1 -> B

第44手
3 -> C

第45手
1 -> A

第46手
2 -> C

第47手
1 -> C

第48手
5 -> A
これで左端に2枚移動できました。もう一息です。

第49手
1 -> B

第50手
2 -> A

第51手
1 -> A

第52手
3 -> B

第53手
1 -> C

第54手
2 -> B

第55手
1 -> B

第56手
4 -> A
左端に三枚移動完了。残り3枚となると、もうできたも同然ですね。

第57手
1 -> A

第58手
2 -> C

第59手
1 -> C

第60手
3 -> A

第61手
1 -> B

第62手
2 -> A

第63手
1 -> A
完成!
ということで、63手でした。
これは実際にやってみると面白くてくせになり何度もやってしまいます。ここでの例は右から左への移動でしたが、右から中央、左から右、左から中央などと始点と終点を変えるとさらに面白味が出てきます。
ちなみに、枚数と最小の手数は以下のようになります。
| 枚数 | 手数 | 計算式 |
|---|---|---|
| 1枚 | 1手 | 2^1-1 = 2-1 = 1 |
| 2枚 | 3手 | 2^2-1 = 4-1 = 3 |
| 3枚 | 7手 | 2^3-1 = 8-1 = 7 |
| 4枚 | 15手 | 2^4-1 = 16-1 = 15 |
| 5枚 | 31手 | 2^5-1 = 32-1 = 31 |
| 6枚 | 63手 | 2^6-1 = 64-1 = 63 |
| 7枚 | 127手 | 2^7-1 = 128-1 = 127 |
| 8枚 | 255手 | 2^8-1 = 256-1 = 255 |
なんだかプログラマーにとってはなじみの数字に近い物が並んでますね。そうなんです、最小手数は2の枚数乗マイナス1となるのです。
ハノイの塔に関してもっと知りたい方はこちらをどうぞ。元々は64枚なのだそうで、実際に動かそうとしても生きている間には絶対に完了しません。
2015年9月26日 記